令和4年3月11日: 東日本大震災トリアージ訴訟を掲載
Σ とは？
今ここに，数列
があるとする。さて，この数列の第n項までの和というのは，
のことであるが，この表し方だと「この数列の第5項から第20項までの和」というものは一発では表せない。そこでそれを表すために考え出されたものがΣ (シグマ)記号である。１ずつ変わっていく部分を適当な文字で身代わりしてもらい（ここではkを使う），「Σ 」の下と上に，その文字が何から何まで次々に変わるかを示して，
と表すのである。
(Σ の下の「
」が「kは5から」を，Σ の上の「20」が「20まで」を表す。)
ところで，ここで注意すべきことは，上の式の文字kは，5から20までの数字の単なる身代わりであるから，別にkでなくても構わない，ということである。例えば
は，
や 
や 
と全く同じなのである。どの式も展開すれば，つまり文字の部分を5から20まで次々に変えていって全部を足せば，できる和の式は同じなのである。そこで，目の前にあるΣ が何を表すかを的確につかむには，「このΣ を展開したらどうなるか？」を常に考えることが重要である。例えば今登場した
であれば，kに5 , 6 , ……, 19 , 20を次々に代入して足すと
となることが即座にわかることが必要である。
ところでΣ でまとめられるのは，
の中の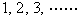
の部分，つまり数列の添字，だけにとどまらない。例えば
のように，次々に１ずつ増えていく部分がある数列の和であれば，その部分を適当な文字で身代わりしてもらえば，
とまとめることができるのである。
逆にこの
が与えられたときは，kに
を次々に代入して足すと，
となることが即座にわからなければならない。
おまけ話であるが，数列の和をΣ で表すなら，数列の積はどうか，というとこれにもちゃんと記号があって，例えば数列{an}の第5項から第20項までの積は，
と表すのである。因みにΠはギリシャ文字πの大文字である。
